Retrouvé ça


Ou je fais court et j'affirme, ou j'essaye de faire passer ce que je crois avoir compris et ça sera plus long ! Allons y !

Aucun composant n'est pafait.

Une résistance présente toujours pour le moins une valeur "selfique" en série et une valeur "capacitive" en paralelle.

Un condensateur possède aussi une self et une résistance série ainsi qu'une résistance paralelle.

Dans le domaine audio, c'est à dire pour des fréquences comprises entre 20Hz et 50KHz, ces défauts et leurs conséquences sont souvent négligeables.

Un transfo de sortie n'est pas un composant aussi "simple" qu'une résistance ou un condensateur.
Il contient une certaine quantité de fils de cuivre enroulés sur un noyau magnétique.
Il est déjà évident que ces fils sont résistants. Comme ils sont trés voisins il y aura aussi quelque part un effet capacitif et puisqu'ils sont enroulés sur un matériau magnétique, des selfs vont apparaitre.

Dans ce genre de situation, il est pratique de supposer un composant parfait autour duquel on ajoute des composants parasites représentant ses imperfections.

En simplifiant à l'extrème un transfo peut être représenté ainsi:



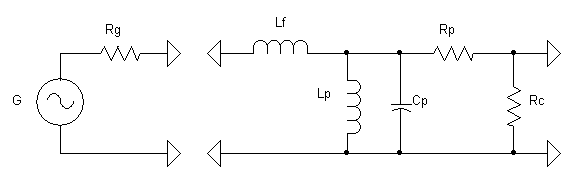
De gauche à droite:

(Ne faisant pas partie du modèle de transfo) Un générateur "G" et sa résistance interne "Rg" qui représente le tube (lui non plus n'est pas parfait !)

Une self en série "Lf" qui représente l'inductance de fuite (Leakage inductance)
*** Ceci représente les imperfections de couplage entre le primaire et le secondaire qui augmentent avec la fréquence.
Pour simplifier, disons que cela provient de la distance entre les premières et les dernières spires.
***

Une self en paralelle "Lp" qui représnte l'inductance du primaire

Un condensateur en paralelle "Cp" qui représente l'ensemble des capacites réparties

Une résistance en série qui représente l'ensemble de la résistance ohmique des enroulements

Et enfin "Rc" qui est la résistance de charge affectée du rapport de transformation.

Pour rester concret, prenons des valeurs "plausibles".

Rg : 1700 Ohms (Rp moyen d'une 845)
Lf : 15mH
Lp : 20H
Cp : 500pF
Rp : 300 Ohms
Rc : 9000 Ohms

et voyons quelle est la charge effectivement présentée au générateur (Zeff).

Quelle que soit la fréquence, on a déjà Rp en série avec Rc = 9300 Ohms.
Donc la résistance des enroulements vient augmenter l'impédance effective (en pures pertes).

Pour 50Hz:
ZLf = 15mH x 6,28 x 50 = 4,7 Ohms
ZLp = 20 x 6,28 x 50 = 6280 Ohms
ZCp = 1 / (6,28 x 50 x 500pF) = 6,4 MOhms

on peut négliger ZLf et ZCp, on n'a plus que ZLp en paralelle sur Rp et Rc :
Zeff = 1 / ((1 / 6280) + (1 / 9300)) = 3748 Ohms.
La puissance fournie alors dépend de l'impédance du générateur (Rp : 1700 Ohms) qui forme un diviseur de tension avec Zeff.
Ici l'attenuation en tension est (1700 + 3748) / 3748 = 1,45, et en puissance (1,45²) = 2,11.

Pour 1Khz:
Zlf = 94,2 Ohms
ZLp = 125 KOhms
ZCp = 318 KOhms et donc Zeff = 8330 Ohms. Là ça va pas mal.

Pour 20Khz:
ZLf = 1884 Ohms
ZLp = 2,5 Mohms
ZCp = 15923 Ohms, Zeff est maintenant 9300 en paralelle avec 15923, le tout en série avec 1884 = 7755 Ohms.
La charge se trouve en paralelle avec Cp et la tension reçue est divisée par (1884 + 5870) / 5870 = 1,32, la puissance réduite dans un rapport de 1,7.

Etc... etc ......
Dans le monde réèl, je pense qu'il y a plusieurs inductances de fuite et plusieurs capacités parasites réparties tout au long de Lp.

J'ai bien relu, j'espère que je me suis pas trop gourru !

Yves.

Bonjour Yves
Effectivement tu as fait court et il me semble que tu as raison.
Un transfo de sortie demande des calculs bien sûr mais c'est aussi
une autre alchimie.Je crois que tout ne peut-être quantifié ce qui explique
certaines réussites ou échecs.
Et encore tu considères,à juste titre, le TS pris isolément mais si on le plonge entre l'étage final et les HP avec leurs fcem etc !!!
Il y a qques temps avait été évoqué l'article de Walter-Chrétien dans
l'Audiophile 39.C'est cet article qui m'avait décidé à acheter des U808 Tango après avoir hésité(regrets) sur la commande des Partridge.
J'avais fait des essais avec des KT88 Gec en trétrode ou triode
sans CR bien-sûr.Du bas médiumà l'extrême aigu:remarquable à mes oreilles bien sûr.
Puis abandon avant essai sur des triodes vraies que je n' avais pas pu
trouver immediatement.
As-tu essayé ces transfos?
Ceci dit je crois aussi,vu la dépense,que des caractéristiques minimum
devraient être publiées Je pense en avoir davantage sur un TU101 que sur tous les autres!!
Cordialement
JC

Yves,

Très bonne idée d'avoir republié ton excellent message concernant les transfos.
J'avais commencé à le retaper et allais te demander si je pouvais le publier sous ton nom.
Inutile donc .....
As tu également la suite qui concernait les conséquences sur le calcul du facteur d'amortissement et l'impédance de sortie vue par le haut parleur?
Il me semble interessant de développer un peu cela.

Bien à toi.

Pascal,

Ce qui vient de se passer doit évidemment nous servir de leçon et nous permettre d'améliorer le fonctionnement du forum.
Comme je l'avais suggéré, cela ne montre t-il pas qu'il y aurait un intérêt à distinguer les post qui concernent la vie du forum au jour le jour et ceux qui, faisant référence, pourraient faire l'objet d'un traitement sécuritaire particulier.

Kikoo !


Petite question, pas trop hors sujet j'espere, et orientée push-pull.

Je vois regulierement des shemas qui pour une meme lampe et un point de fonctionnement voisin, utilisent des transfos de sortie d'impedance tres éloignée.

Etant de plus en plus branché calcul plutot que recopiage, comment déterminer l'impédance?

Et là je vais en faire crier plus d'un...

Si ce fameux (j'espère!) transfo est connecté à la cathode, que devient l'impédance ?

Aie !

Bonjour,

Je profite de ce fil sur les transfos de sortie pour relancer une discussion qui avait eu lieu avant les "évènements" de dimanche et qui a disparu.

Après avoir monté pas mal d'amplis SE et PP avec des transfos Magnétic (ESO) qui m'ont donné toute satisfaction, je démarre la conception et la fabrication d'un intégré SE 211.

Voulant éventuellement essayer autre chose, et comme, au contraire de certains "velus" de ce forum, je n'ai aucune compétence en matière de bobinage, j'ai fait une demande de prix chez Hexacom pour des transfos 9K/8ohms adaptés aux tubes 845 et 211.

Les prix sont sensiblement du même niveau que ceux d'ESO, mais ils me proposent une carcasse EI M6X ou double C M6X, cette dernière étant un peu plus chère.

Y a-t'il une vraie raison objective qui devrait me faire préférer le double C à l'EI?
Il me semble que tous les transfos que j'ai fait faire chez Magnétic étaient des EI.

Je crois me souvenir que certains avaient fait des mesure du respect de l'impédance (et de bande passante?) des transfos Hexacom, Magnétic, ...
Je ne me souviens plus des conclusions.

Avant de passer commande, j'aimerais bien être rassuré

Diafan

Yves07, Toi qui a l'air d'en connaitre un brin sur les transformateurs, est ce que tu pourais eventuellement en parler un peu sur le wiki ?

j'ai créé une categorie "Les Composants" et dedans j'ai déja créé "Les Transformateurs" ... ce serait chouette si tu pouvais editer la page et faire un copier/coller de cet article

si la mise en page n'est pas parfaite, c pas grave je repasserais apres toi
merci

c'est ici: http://cabestan.be/wiki/index.php/Les_Composants
il te suffit de t'enregistrer (en haut a droite, connection) et ensuite de cliquer sur le lien 'Les Transformateurs'
merci.

Bonjour a tous.
Sur le sujet transfo de sortie historiquement les circuits en C ont surtout été inventés pour simplifier la vie du bobinier!!!!! car procéder a l'entôlage d'un transfo PP par exemple ce n'est pas de la tarte!!!!! il faut vérifier chaque tôle au niveau du sens de la bavure serrer au max les tôles entr'elles sans les déformer etc...... j'ai lu beaucoup de choses sur le sujet et j'en suis presque arrivé a la conclusion que la soi disant supérioté du circuit en C/ aux tôles est surtout commerciale!!!!!
La tôle EI M6X employée pour les bons transfos de sortie est la même que celles des circuits en C.D'une manière générale a encombrement égal il y a plus de fer dans un transfo EI que dans un transfo utilisant des circuits en C je tiens ces infos de 2 éminences faisant partie de mes relation.
Si je peux me permettre un dernier conseil attention a la provenance des circuits en C j'ai refait (a l'identique)un transfo d'alim pour un double PP de 6550 qui était a l'origine un Chrétien en achetant les circuits chez un bobinier Français eh bien il m'a vendu une merde!!!! je m'en suis aperçu en faisant une mesure particulière en le comparant a un Métal Imphy de la même taille c'était le jour et la nuit... je m'en suis sorti en achetant ce qu'il me fallait comme circuit chez Telmag en Angleterre qui m' a donné le même niveau de performances que le Métal Imphy.
A bientôt.
Cordialement.
gege 94

Il y a plusieurs façons de charger le même tube, en changeant ou pas le point de fonctionnement, selon ce que l'on cherche à obtenir.
Récupère les courbes d'anodes et trace des droites de charges !
Dans la réalité, le haut parleur est tout sauf une résistance et la droite de charge tourne vite à l'ellipse selon la fréquence considérée.
C'est la vie, faut faire avec



Exactement la même ! ! ! Les tensions aux bornes du tube et les courants y circulant ne changent pas, et pour le transfer de puissance l'impédance de charge doit rester identique.
Par contre le coefficient d'ammortissement s'amèliore considérablement.
Le gain en tension du tube devenant sensiblement égal à 1, le driver a du boulot !

Yves.

Et moi j'en profite pour continuer de déplorer la non disponnibilité des caractéristiques
Avec l'age, le radotage deviendrait il une seconde nature
Bien sûr, on pourrait les mesurer, mais ce serait plus "politiquement correct" que le constructeur publie lui même ses données "officielles".

Plus concrètement, le "papier" avance, mais c'est long !
Par chance, j'ai trouvé un volontaire pour relire mes élucubrations.
Ca vient, ca vient.
Il y aura un chapitre sur la façon de les mesurer

Yves.

Yves, tu n'aime pas le wiki ? allééééééééé c pas dur

il suffit de S'inscrire
et puis de éditer la page sur les transfos

Bonjour a tous.
Je lis avec attention les différents posts sur le sujet en adoptant une prudente réserve et je compare a ma littérature dédiée .
OK pour les caractéristiques mais lesquelles?
Pour que la chose soit lisible il faudrait que tout le monde parle le même langage !!! ce qui est loin d'être le cas un exemple la mesure de la distorsion harmonique tous les amplis de 50Watts mesurés a 0,1 Watt sont bons!!!! même pour les signaux carrés.
Ce qu 'il faut a mon avis c'est dégager des caractéristiques majeures du genre self primaire pour autant aussi qu'elle soit mesurée de la même façon en fréquence et en tension avec ou sans composante continue.
La taille du circuit magnétique a aussi son importance la résistance ohmique du primaire la self de fuite les capas réparties et le mode de sandwich primaire secondaire ainsi que leur nombre se rappeler aussi qu'un transfo de sortie SE a ses éxigences qui ne sont pas les mêmes que celles d 'un transfo PP et d.'un transfo de liaison etc etc. Comme dirait l'autre un violon est fait essentiellement de bois il existe de par le monde une kirielle de luthiers pourtant a ma connaissance personne n'a encore égalé Stadivarius.
A bientôt.
Cordialement.
gege 94

Oui Gérard !

C'est bien comme ça que je vois les choses.
Les chiffres doivent être clairs, lisibles et le contexte ainsi que le mode de mesure parfaitement défini, connu et reproductible.

Ensuite, leur interprétation est laissée aux préférences de chacun.

Comment le fabriquant a t'il obtenu telle ou telle performance est certes interressant, mais on entre alors dans le domaine de la propriété intellectuelle.

Ce qui n'empèche aucunement de décrire les méthodes de base ainsi que les incontournables compromissions permettant d'aboutir à un produit équilibré.
Faire un inductance primaire enorme avec peu d'indution OU une inductance de fuite ridicule avec des capas parasites faibles sont deux choses très faciles .... tant qu'on essaye pas d'avoir les deux en même temps

L'ai je bien repondu ?



Feeling,

Je suis déjà inscrit, mais laisse moi un peu de temps



Yves.

OOps désolé c'est juste que je trouverais ca sympa que tout le monde puisse proffiter d'une superbe base de conaissance
et je suis contant que des gens comme toi y participe
tu as tout le temps

A+

Merci à ceux qui m'ont répondu, sur ce fil et en privé.

J'ai pris la décision de commander des transfos bobinés sur carcasse double C chez Hexacom.

Comme j'ai déjà un ampli SE 845 équipé de transfos EI Magnétic, j'aurai toutes facilités pour les comparer.
Je ne manquerai pas de faire part ici de ce match.

Problème: si les transfos Hexacom se révélent meilleurs que les Magnétic, il sera difficile de savoir si c'est à cause de la forme de la carcasse (clin d'oeil à Gege94) ou à cause du savoir faire du fabricant!

Mais il est certain que la publication des caractéristiques détaillées des transfos par leurs fabricants nous faciliterait les choses...

Diafan

Bonsoir,
c'est peut être un peu hors sujet mais ça parle toujours de transfos:

savez vous OU peu on trouver des transfos Hammond en France? pas hors de prix si possible

merci d'avence

Vincent